排列五与概率论的关系
排列五作为一种广泛流行的彩票游戏,吸引了众多彩民的参与。在这类彩票中,玩家选择5个数字(从0到9),并按一定顺序排列,最终中奖的方式通常是根据开奖号码与玩家所选号码的匹配情况来确定。这种类型的游戏涉及到概率论的基本原理,特别是组合、排列、事件发生的概率以及期望值等概念。本文将探讨排列五彩票的概率论基础,分析其概率分布,并通过实际计算帮助读者深入理解其背后的概率机制。

一、排列五游戏的基本规则
排列五彩票是一种数字排列游戏,具体规则如下:
- 号码选择:玩家从0到9的数字中选择5个数字,并且需要指定每个数字的具体位置。
- 中奖方式:玩家的号码与开奖的号码完全一致,且顺序相同,即为中奖。
- 中奖几率:由于彩票号码选择的数字顺序很重要,因此,排列五属于排列类问题而非组合类问题。
例如,若开奖的号码是“12345”,玩家如果选择了“12345”,则为一等奖中奖。
二、排列五的概率分析
排列五的核心是排列问题。假设一个排列问题的基本条件是:从n个元素中选取r个元素进行排列。在排列五中,n=10(即数字0-9)且r=5(即选择5个数字),因此,排列五的总可能数为:
1. 排列数公式
排列数的公式为:
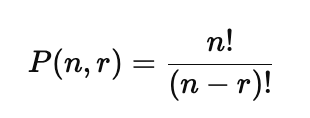
对于排列五来说,n=10,r=5,所以:
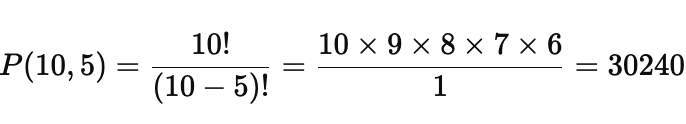
因此,排列五的总可能组合数为30240种。
2. 单注中奖概率
排列五的中奖是根据玩家选择的号码与开奖号码完全一致来判定的。由于共有30240种可能的结果,而玩家仅选择一种号码,因此中奖的概率为:
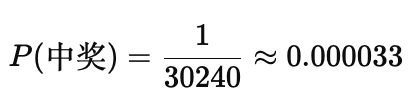
这意味着,每注投注的中奖概率大约为0.000033,即0.0033%。这也表明,排列五的中奖概率非常低。
三、概率论中的相关概念与排列五
1. 期望值
期望值(Expected Value)是指在一个随机事件中,所有可能结果的概率加权平均值。在排列五彩票中,我们可以计算其期望值来评估玩家的平均收益。
假设排列五的单注投注金额为2元,一等奖的奖金为100万元。那么,期望值计算如下:
E(X)=P(中奖)×奖金+P(不中奖)×亏损金额
其中,P(中奖) = 1/30240,奖金 = 1000000元,P(不中奖) = 30239/30240,亏损金额 = 2元。因此,期望值为:
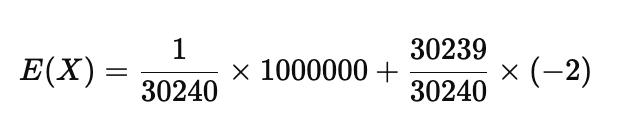
E(X)=33.06−2.00=31.06
这意味着,每注投注的期望值大约为31.06元,表示玩家在长期参与中,每注投注平均会亏损31.06元。可以看出,排列五彩票是一项负期望的游戏,长时间投注会导致玩家的亏损。
2. 大数法则
大数法则指出,随着重复实验次数的增加,实验的平均结果会趋近于理论期望值。在排列五的情况下,如果一个人进行大量投注,他的长期平均损失会逐渐接近期望值。例如,如果某彩民投注了10000注,理论上他应亏损大约31060元。这种趋势在大规模投注中尤为明显。
3. 组合与排列
排列五彩票的问题涉及排列,而非组合。排列与组合的主要区别在于是否考虑顺序。在排列问题中,顺序是非常重要的,而在组合问题中,顺序不重要。排列五中的中奖条件要求玩家选定的5个数字顺序与开奖号码完全一致,因此这是一个典型的排列问题。
四、排列五的概率分布
1. 二项分布
尽管排列五的中奖概率极低,但它仍可以用概率分布进行描述。在这种情况下,每次投注的“中奖”或“未中奖”可以看作是一个伯努利试验,其结果为“成功”(中奖)或“失败”(未中奖)。在进行多次独立投注时,排列五的中奖情况可以用二项分布来描述。假设进行n次独立投注,每次投注的中奖概率为p,则中奖的次数X服从参数为n和p的二项分布,即:
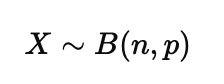
其中,n为投注次数,p为中奖概率(p=1/30240)。
2. 泊松分布
如果投注次数非常大(例如上百万次投注),那么中奖次数的分布可以近似为泊松分布。泊松分布适用于描述在固定时间或空间区域内事件的发生次数,特别适用于稀有事件的模型。在排列五的情况下,中奖事件的发生是一个稀有事件,可以使用泊松分布来近似描述。
五、排列五的策略与优化
由于排列五的中奖概率非常低,玩家不可能通过常规手段增加中奖的概率。不过,一些优化策略可以帮助玩家合理规划投注,以最大化期望收益。
1. 多注投注
通过多注投注,玩家可以在理论上增加中奖的概率。例如,如果玩家购买了10注号码,每注号码的中奖概率为1/30240,那么10注号码的中奖概率将增加到10/30240。虽然这仍然是一个极低的概率,但至少能够稍微提高中奖的机会。
2. 集体合买
一些彩民会选择集体合买,即通过集体资金购买更多注号码,以此增加中奖概率。这种方式实际上是一种分摊风险的策略,虽然中奖几率提升,但每个成员的奖金会被平分。
3. 理性投注
从概率论的角度来看,理性投注应基于期望值的计算来决定投注金额。在负期望的情况下,理性玩家应避免过度投注,而应将其视为一种娱乐方式而非赚钱的手段。
六、总结
排列五作为一种彩票游戏,充分展示了概率论的应用,尤其是在排列、组合、概率分布以及期望值等方面。虽然其中奖概率极低,但通过合理的投注策略和对概率的理解,玩家可以更好地认识到彩票的风险与收益。在这种低概率的游戏中,保持理性并充分理解概率论的基本原理,是参与其中的最佳方式。